丙加·第8章·一人千役（函数与参数）

本章将讲解函数的基本知识。包括函数的定义、重载（C++）和参数的传递方式（C 的指针、C++的引用）等

8.1 函数千面，奔走人间
#

在《崩坏：星穹铁道》中，花火拥有“一人千役”的能力。而我们的函数同样可以做到“一人千役”。这里“役”有两种理解方式：第一种是日语中“角色、职位”之意：同一个函数名，却能根据不同的“剧本”（参数列表），扮演不同的“角色”（执行不同的功能）；第二种是汉语的字面意思：函数的作用就是将重复、常用、功能性强的代码片段包装起来，一次又一次使用 ~~GO WORK!!!~~。本章，我们就来学习如何让我们的函数成为这样的千面英雄。

8.2 Le clou du spectacle: 函数的声明与定义
#

函数往往是一些常用代码片段的包装，以方便我们反复使用一个功能。比如说“贯耳冲击”、“抓腕砸肘”等就可以看成一系列函数，“擒敌拳”又可以看成包装了“贯耳冲击”、“抓腕砸肘”等动作的函数 ~~（大雾）~~。前者的函数体包含肢体的运动，口号的呼喊，平衡的调节等内容，当我们说到“贯耳冲击”，就知道这是一个“进步贯耳、右膝冲击、落步肘击并附带口号”的整体过程了；说到“擒敌拳”，就知道是从“贯耳冲击”到“摆勾冲膝 ”的 16 个动作了 ~~——这就是函数带来的便利啊！（弥天大雾）~~

函数的开幕非同凡响。我们往往这样声明：

// 返回值类型 函数名(类型 参数名称1,类型 参数名称2, 更多参数……);
int absolute(int number);

当然，其实编译器只关心返回值类型、函数名和参数的类型（后两个就称为一个函数独一无二的“签名”），所以很多代码也会这样写：

int absolute(int);

声明完毕后，编译器便知道“有这样一个函数”。于是函数的具体内容，也就是函数定义就呼之欲出了。参照我们打算写的绝对值函数 absolute 的声明，absolute 函数的定义可以这样写：

// 第一行**目前**可以说是抄一遍，别打分号
int absolute(int number) {
    // 内部就是函数对传入数据的一系列操作，
    // 然后使用return结束函数执行
    // 并返回运算结果（如果返回的不是void）
    
    // 演示上一章的三元表达式
    return (number > 0) ? number : -number;
}

碎碎念: 函数声明其实是可选的。目的是将声明与函数体分开来，方便快速查看和管理——对于较短较简单的函数，我们可以选择只写定义。一般地，函数的声明会放在 xxx.h 里面，而实际的定义位于同名的 xxx.cpp（或者 xxx.c）中。函数的声明目的是告诉编译器有这么回事，请在别处寻找它的定义，这有可能是 cpp，可能在其他包含的项目目录，甚至是其他语言的导出函数，没有代码形式的函数体！所以编译器相对比较佛系，只有需要（函数真正被使用）的时候才会寻找这个符号，把它加入最后的程序中（称为“链接”）。

如果函数只有声明而没有定义，但是这个函数没有被使用，那么不会产生错误（因为编译器压根不会关心它的死活）。
void akari(void); // 声明而没有定义

int main() {
    // akari();
    return 0;
}
但一旦你尝试使用它（比如取消注释上面的那一行），那么编译器就会突然发现没这个函数，于是会产生类似这样的错误：
undefined reference to 'akari'
如果声明与定义不匹配，在 C 中会直接报错，而 C++会更复杂些：
void foo(int x); // 声明：参数为 int

// 定义：参数为 double
void foo(double x) { 
 // ... 
}
   
int main() {
 foo(10); // 调用哪个？
 return 0;
   }
编译器认为你这是想重载（看不懂的完成下一节再回来吧）函数 foo，而参数列表 int 和 double 确实是不同的，所以理论上可以重载。然而，这里只提供了 double 版本的定义，却没有提供 int 版本的定义。当你调用 foo(10) 时，编译器找到了一个声明 void foo(int)，但却找不到它的实现，最终还是会导致 undefined reference 链接错误：
undefined reference to `foo(int)'

8.3 La déesse aux cent miracles: 函数的重载（C++）
#

在 C 语言中，一个函数名只能对应一个函数体。这带来了一些不便。比如在 math.h 中，就定义了 abs、cabs、labs、fbs 等等函数，分别用于计算整数、字符、长整数、浮点数的绝对值，而没有办法统一地调用（重复之前的说明，我们不讨论 C 对泛型、面向对象复杂笨重的模仿——它说到底还是面向过程的语言）。C++提供了多种方案来解决这类麻烦事。我们这次先学习其中一种——函数重载。

所谓重载（Overloading），就是重新装载（over 应该理解为 over again 而非 too much）——一个函数名装入新的、不同的定义。函数重载其实和函数声明写起来没什么差别——只是函数名重复了而已。我们延续前面 absolute 函数的例子，写一个对应的 double 版本：

int absolute(int number) {
    return (number > 0) ? number : -number;
}

double absolute(double number) {
    return (number > 0) ? number : -number;
}

这样，C++编译器会生成两个 修饰名：_Z8absolutei 和 _Z8absoluted（_Z: 前缀；8: 函数名 absolute 的字符长度；i 和 d: 参数类型代号，i 代表 int，d 代表 double）。编译的时候，编译器可以根据传入的变量类型决定使用哪一个函数，函数重载就这样完成了。

不过，这样的重载是不可以的：

int absolute(int number) {
    return (number > 0) ? number : -number;
}

double absolute(int number) {
    return (number > 0) ? number : -number;
}

原因很简单，上面也提过了，编译器没办法根据传入的变量类型决定使用哪一个函数。

碎碎念：

其实这样的场景下，使用“模板”来自动生成不同的重载是个更好的选择，看不懂没关系，我们后面会具体学习。不过你可以尝试模仿它，用它完成课后习题。
// 用T来指代通用的类型名
template <typename T>
T absolute(T number) {
    return (number > 0) ? number : -number;
}
这样，只要传入的类型有大小比较、加减正负运算，就能直接套用这个模板。~~有公式做题就是快！~~

也可以使用 2 个以上的通用类型，下面的 max 就可以接受 int 与 double 的比较
template <typename T, typename T2>
T Max(T a, T2 b) {
	return a > b ? a : b;
}
上面的代码就是所谓的“泛型编程”，“泛型”可以理解为“通用类型”。

8.4 La marée s‘invite à la fête: 函数的参数
#

很多函数接收一系列参数，而我们在变量、指针等章节中已经或多或少接触过参数的传递。我们现在来正式学习它。
参数的传递主要有 3 种：按值传递、指针传递、引用传递。

8.4.1 按值传递
#

这是最简单的传递方式，变量拷贝一份以后送入函数。前面的 absolute 就是这种传递方式，故我们不再举例。

但是这种方式有其局限性：

无法修改外部变量的值：传入的参数是一个副本，如何折腾都不会影响外部。
大型变量拷贝较慢：对于自定义的较大的类（比如包含大量成员、方法等等 ~~一车面包人~~），如果每次传入都拷贝一次，势必会产生较大的开销
复杂类型拷贝不彻底：按值传递执行的是“浅拷贝”，浅在何处？举个例子：如果定义了一个包含指针成员的类，浅拷贝的时候 只复制指针本身，而不复制指针指向的数据，所以里外两个变量内部其实指向了一个东西——如果操作指针，就会修改到那个共有的地址。这一般不是我们所想要的。更糟糕的是，如果这个类变量是自主管理内存的，一旦函数结束，内部变量就会释放一次指针指向的那片内存区域，导致外部变量的指针悬空。造成更严重的问题。

这种时候，就需要指针，或者更现代的引用出场了。按值传递的剧目就先到此为止。

碎碎念：

如果你想防止修改传入的那个副本（并不是为了防止修改外部的原变量），可以使用 const 修饰符。这可以比较有效地防止在函数内部 意外地 修改了那个副本，从而避免引入逻辑错误。如果你不小心写了修改它的代码，编译器会直接报错。

#include <iostream>
#include <string>

void printStringInfo(std::string str) { // 按值传递，发生拷贝
    // 函数本意只是读取，但下面这行意外的修改也能通过编译
    // 意外修改！虽然这只修改了副本，不影响外部原变量
    // 但是影响了程序的逻辑
    // 别看这个很傻，但是在长的程序中极容易出现
    // 比如你原本将传入的参数作为原始样板
    // 但是后面突发奇想想要进行一些处理
    // 这样样板就被污染了
    str[0] = 'X'; 
    
    std::cout << "Length: " << str.length() << std::endl;
    std::cout << "First char: " << str[0] << std::endl;
    // 输出变成了 Length: 11, First char: X
}

int main() {
    std::string myGreeting = "Hello World";
    printStringInfo(myGreeting);
    std::cout << "My string is still: " << myGreeting; // 输出 Hello World，未被修改
    return 0;
}

上面的代码直观的展示了这个问题

如果我们使用了 const：

void printStringInfo(const std::string str) { // 使用 const 修饰按值传递的副本
    // str[0] = 'X'; // 如果尝试修改，编译器会立刻报错！
    // 错误信息：error: assignment of read-only location ...

    // 读取操作是完全允许的
    std::cout << "Length: " << str.length() << std::endl;
    std::cout << "First char: " << str[0] << std::endl; // 输出正确的 'H'
}

就可以避免这样的问题

8.4.2 指针传递
#

这是 C 语言提供的修改外部变量的方式，如第六章所属，像 scanf 就是采取这个方式修改传入的变量，达到读入的目的。我们这里再复习下第六章的内容：

void square1(double num) {
    num *= num;
}

void square2(double* num) {
    (*num) *= (*num); 
}

int main() {
    // 提一嘴：这里的num和square函数的num不是一个num
    // 一个在main()，一个在square()
    // 专业地说，这叫“位于不同的作用域”
    double num = 3.14;
    
    square?(num);
}

看看哪个函数（square? 处）可以达到将传入的数字平方的目的。如果你不清楚，请务必先回去复习下第六章。

8.4.3 引用传递
#

这是 C++中提供的方式，结果是内外两个变量其实使用的是同一片地址，这和指针有点像，但是不需要解引用。引用变量使用的是 &：

void square3(double& num) {
    num *= num; 
}

可以很自然地操作外部变量。

但是恰恰是由于它太自然了，更容易发生意外修改而且影响外部原变量的错误，这比 8.4.1 更严重。所以，在确定函数不会修改外部变量的时候，请 务必记得使用 const。（当然，const int* num 这种的确不能修改 *num 了，但是 num 本身也有可能不小心修改，还是有点风险的——这也是 C++推荐使用引用的原因之一）。 关于 const int* 和 int const* 参见 6.2.1 结尾

补充一嘴，引用变量其实不仅仅可以在函数定义时使用，只是在函数定义中使用最为广泛：

int var1 = 999;
int& var2 = var1; // 引用变量必须定义的时候就绑定一个变量名（值当然不可以啦~）
var2 = 99;        // 这样var1就变成了99，var2看起来就像var1的别名

碎碎念：右值引用（C++11）

看一个反直觉的代码：
int &&r = 10; // 右值引用绑定字面量
r = 20;       // 修改右值内容
这看起来很奇怪：右值 10 不是临时的、不可修改的吗？为什么能绑定还能修改？

其实当你开始使用右值引用 && 时，这个 10 就被提升为一个隐藏的变量了，相当于：
int __temp = 10;    // 编译器生成的临时变量
int &r = __temp;    // r 实际引用这个变量
r = 20;             // 修改 __temp 的值
如果我们构造了一个超大的、内部包含指针的临时变量，进行深拷贝就必然要将指针指向的值再拷贝一次。但是临时变量是要被销毁的，我们可不可以废物利用下，减少拷贝的开销呢？&& 正是为此而生的：它将一个类似 10、{1123, "阿爸阿爸八八八八八八八八"} 的临时的、看似不可修改的右值提升为变量，然后变拷贝为移动（这叫做 移动语义），直接接管其内存，这样就大大提高了程序效率。

8.4.4 形参和实参
#

在讨论函数参数传递时，有两个关键概念需要区分：形式参数（形参） 和 实际参数（实参）。

听着很绕，实际上不太复杂：形式参数就是“门面”，是在 函数定义（函数声明时的变量名会被忽略，编译器那时只关心类型）时，声明在函数括号内的变量——它是函数内部的局部变量，也就是我们之前一直说的“内部变量”；而实际参数则是调用函数的时候传入的那个变量，也就是之前说的“外部变量”。

函数调用时，实参会按照函数定义中指定的传递方式（按值、指针、引用）来初始化形参。这个过程就是一直在提的 参数传递（也有叫 参数绑定 这样的说法）。当 按值传递 时，实参会被（浅）拷贝一份给形参；当 指针传递 的时候，实参的地址被复制给形参（其实就是按值传递一个指针啦）；特别地，引用传递 时，形参成为实参的一个别名。它们指向内存中的同一个地址，操作形参就是直接操作实参。

补充知识：默认参数

可以在声明或定义函数时指定默认参数。像这样：
int func(int a=1) {
   ...
}
这样一来，func() 就等效于 func(1) 了。

注意，声明和定义只能有一处指定默认参数。像这样是会报错的：
int func(int a=1);

...

int func(int a=1) {
   ...
}
读者可以根据习惯选一个位置指定默认参数。

8.5 Acta est fabula, plaudite: 函数的返回
#

函数执行完毕后，就会交换控制权给上家，并（可能）顺便携带一个值传递计算结果，这就是返回（return）。

一般使用 return 语句返回函数，执行到 return，函数就会立即结束。return 的语法如下：

return 返回值;

如果返回类型是 void，也就是没有返回值，那么直接 return; 就好了，或者也可以不写：在函数结尾，相当于有一个 return;。

编译器会尝试对返回值进行允许的自动转换，比如函数返回 double，但是你 return 一个 float，那么就会触发自动转换。不过降级的转换（double-> int 之类的），即使可能可以自动（C 要宽松些），最好还是采取强制转换的方式。

碎碎念：副作用？主要作用？

在我们前面的很多例子中，函数的一个重要目的似乎是修改外部变量的值（通过指针或引用），或者是执行一些操作（如打印信息）。这可能会带来一个疑问：函数的主要作用到底是什么？

想不到吧，其实是 返回值，而不是中间发生的各种现象！

其实这倒也不奇怪——从最“数学”的角度来看，一个 函数（Function） 最本质的角色就是接收输入、进行计算、然后 返回一个结果 嘛。这个返回值是函数执行结果的直接体现。因此像修改外部状态、进行输入输出（如 printf、scanf）、打印日志等操作，在编程术语中反而被称为 副作用（Side Effect）。

这里有一个非常经典的例子：printf("%d", 123); 这个函数有明显的 副作用（在屏幕上打印出“123”），但它的 主要作用 或者说它的返回值是什么呢？其实是返回一个 int 值，表示它成功打印的字符个数（在这个例子中，返回值是 3）。

像 Haskell 和 Mu（常用于金融的编程语言，看起来更像是数学公式）这类函数式编程语言甚至极力避免副作用，以追求程序的纯粹性和可预测性。虽然 C/C++是命令式语言，不强制要求消除副作用，但理解这个概念非常重要。

当然，很多有用的函数根本离不开副作用（没有 printf 的副作用，我们如何在屏幕上看到结果呢？）。所以，我们的目的绝不是要消灭副作用，而是要去 理解并管理它们。

因此，我们要认识到是：返回结果才是函数的主要作用，改变外部变量、进行输入输出等操作都是其副作用。一个函数的核心功能应该先考虑尽量通过返回值来表达。对于必要的副作用，要有清醒地使用并在函数名或注释中清晰地说明，而不是让它们成为隐藏的“惊喜”。

8.6 Dans l’eau, doublement je me reflète: 递归
#

函数内部可以进一步调用其他函数，前面我们已经在 main 里面调用了很多函数了；当然一个函数也可以调用自己，这种情况我们称为递归（Recursion）。

来个经典永不过时的例子：

从前有座山，山中有座庙，庙里有个老和尚，老和尚在给小和尚讲故事：“ 从前有座山，山中有座庙，庙里有个老和尚，老和尚在给小和尚讲故事：“ 从前有座山，山中有座庙，庙里有个老和尚，老和尚在给小和尚讲故事：“ 从前有座山，山中有座庙，庙里有个老和尚，老和尚在给小和尚讲故事：…………

这就是递归，但是因为没有终止条件而无限执行下去。用函数可以这样表示：

void drosteStory() {
    std::cout << "从前有座山，山中有座庙，庙里有个老和尚，老和尚在给小和尚讲故事：“ ";
    drosteStory();
}

当然，因为没有终止条件，所以这个函数层数会越叠越高，直到占满了程序的堆栈运行空间然后爆掉。

尝试给这个函数设置一个终止条件，比如设置只能讲 5 层，5 层以后就结束。那么我们就应该有一个计数器来标记到底套了几层，试试全局变量？

#include <iostream>

int drosteTimes = 0;

void drosteStory() {
    std::cout << "从前有座山，山中有座庙，庙里有个老和尚，老和尚在给小和尚讲故事：“ ";
    drosteTimes++;
    if(drosteTimes <= 5) drosteStory();
    else {
        std::cout << "今天休息不讲了。”";
        return;
    }
    std::cout << "于是故事结束了。";
}

int main(){
    drosteStory();
}

但是全局看着太丑了：drosteTimes 只有 drosteStroy 在使用，但是所有人都能看到并修改，这是危险的。我们试试别的办法？🤓☝️ 将次数作为参数传递怎么样？这样也不用硬编码 drosteTimes < 5，还可以主动设定套娃层数：

#include <iostream>

void drosteStory(int drosteTimes) {
    std::cout << "从前有座山，山中有座庙，庙里有个老和尚，老和尚在给小和尚讲故事：“";
    drosteTimes--;
    if(drosteTimes > 0) {
        drosteStory(drosteTimes);
    }
    else {
        std::cout << "今天休息不讲了。”";
    }

    std::cout << "于是故事结束了。";
}

int main(){
    drosteStory(5);
}

输出：

从前有座山，山中有座庙，庙里有个老和尚，老和尚在给小和尚讲故事：“ 从前有座山，山中有座庙，庙里有个老和尚，老和尚在给小和尚讲故事：“ 从前有座山，山中有座庙，庙里有个老和尚，老和尚在给小和尚讲故事：“ 从前有座山，山中有座庙，庙里有个老和尚，老和尚在给小和尚讲故事：“ 从前有座山，山中有座庙，庙里有个老和尚，老和尚在给小和尚讲故事：“ 从前有座山，山中有座庙，庙里有个老和尚，老和尚在给小和尚讲故事：“ 今天休息不讲了。”于是故事结束了。于是故事结束了。于是故事结束了。于是故事结束了。于是故事结束了。

递归的要点有：

方法：你打算使用递归实现怎样的计算方法，常见的有分治（分而治之，拆解问题为更小的问题）、树和图的遍历（分支、搜索……）、规划类问题等等（这些算法我们后面会学到）；
拆解：如何将达成目标简化为可以使用相似的、套娃式的步骤解决的过程——这往往涉及到数列的递推等知识；
结束：~~再放送：总得有个头啊！~~ 在什么条件下这个递归能够结束，这往往和传入的某个参数有关系。

仍然以斐波那契举例：首先，我们需要计算斐波那契数列的第 \(n\) 项 \(f(n)\)，而我们已经知道对 \(f(n+2)=f(n+1)+f(n)\)，所以不需要什么算法，我们就能直接进行第二步拆解： \(f(n+2)=f(n+1)+f(n)\)，而 \(f(n+1)=f(n)+f(n-1)\)，\(f(n)\) 同理……我们注意到这就是最最直接朴素的递归！要知道 \(f(n+2)\)，只需要计算 \(f(n+1)\) 和 \(f(n)\) 即可，而它们也可以由类似的关系得到，这样的递归关系一直到 \(f(0)=f(1)=1\) 为止（对于 \(n<1\) 涉及解析延拓，这显然在我们讨论范围之外）——这就是第三步，结束了。于是我们很轻松地得到了斐波那契的递归函数。

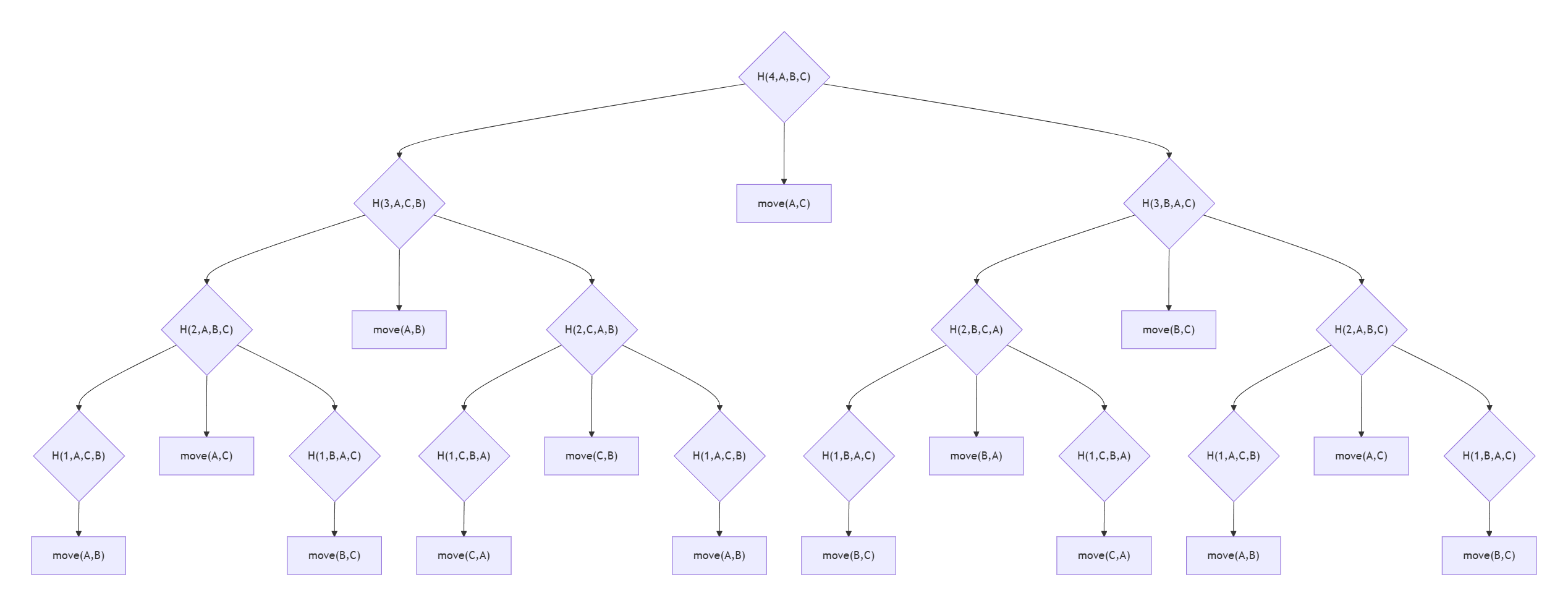
再举一个汉诺塔的例子，我们要把 n 个圆盘从 A 借助 B 移动到 C，记为 H(n, A, B, C)。如何拆解问题？我们尝试从 \(n=1,2,3,4\) 手动操作一次，不难发现：

\(n=1\) 的 1 步操作就是 \(n=4\) 的最后 1 步；
\(n=2\) 的 3 步操作很像 \(n=4\) 的最后 3 步操作，也就是 H(1, A, C, B) + move(A, C) + H(1, B, A, C)——虽然 \(n=1\) 的情况实际没有借助中间柱，但我们仍然可以这么记录；
\(n=3\) 的 7 步很像 \(n=4\) 的最后 7 步（同理）。

不难发现：要将 \(n\) 个盘从 A 借助 B 移动到 C，我们只需要依次把最大的没到位的盘子（编号就是 \(n\)）移到 C 即可，然后问题就转化为 \(n-1\) 的汉诺塔了。而“把最大的没到位盘子移到 C”还可以继续分解，那就是：

把 \(1\sim(n-1)\) 的盘子从 A 移到 B（H(n-1, A, C, B)），于是最下面 \(x\) 号盘就暴露出来了
把 \(x\) 从 A 移动到 C ，以后它就固定不动了（因为它最大，所以上面一切发生的都与它无关）
也就是直接 move(A, C)；
然后再把 \(1 \sim n-1\) 的盘子的移动视为新的汉诺塔（B 柱变成了起始柱，A 成中间，但这不重要：交换上次的起始和中间柱子即可：H(n-1, B, A, C)）；
直到 \(n = 1\)，我们惊喜地发现只需要直接将它移动到目标就好。

🎉🎊🎉 完结散花 🎉🎊🎉！！！！我们成功将复杂的 H(n, A, B, C) 拆解成了递归问题和一个 move(source, dest) 的简单操作

如果有点晕，作出流程图就是这样的：

递归的优点有：

优雅： ~~優雅です！~~：相比线性的循环结构，递归往往代码量更少；
**直观：**对于本身有递推关系的问题写起来更加直观；
**倒序优势：**此外，递归的调用就像书堆，后放上的先被拿起（术语叫“栈”，Stack），对于倒序问题也有一定的优势。

然而，递归的方便是伴随着代价的：上面说过，递归是利用堆栈来实现的，所以套娃的层数越来越多，“书堆”就会越堆越高，最终超过程序的上限而导致错误（堆栈溢出）；此外，函数调用是有（CPU）时间、（内存）空间开销的，层层嵌套必然会有或多或少的损失。对此，有一种“尾递归”的方法：把递归调用放在 return 前面一句，或者就在 return 内“干净地”调用（只调用一次，且不涉及其他任何运算），编译器会对这种情况进行优化，避免堆栈越来越高。

那么如何判断适不适合我们判断是否可以使用递归呢？判断是否可以使用递归呢，其实就是判断问题是否可以拆解为更小的、性质相同的问题。比如阶乘的 \(f(n+2)=f(n+1)+f(n)\) 就是很好的例子。而很多线性操作，比如遍历一个数组、逐个输出字符就不适合递归——因为既没有带来代码的简洁，又额外增加了系统开销，得不偿失！当然，对于过于庞大的操作，即使这个递推关系有多么诱人，也不要使用递归——比如计算第 1000 项斐波那契（函数调用记为 F(x)）：且先不论 1000 层堆栈，计算 F(n) 需要计算 F(n-1) 和 F(n-2)，而计算 F(n-1) 又要计算 F(n-2) 和 F(n-3)……其中存在大量的 重复计算。例如，计算 F(5) 时，F(3) 会被计算 2 次，F(2) 会被计算 3 次，F(1) 会被计算 5 次！当 n 稍大（如 40），计算时间就会长得无法接受。不过这不失为理解递归的原理的经典案例。

当然，递归的性能问题并非“不可调和”的，我们可以采取记忆化的方式完成优化，比如斐波那契数列，我们就能增加一个（静态或全局）数组 long long feb[100];（大一点的数字，\(f(100)\) 肯定超过 long long 范围了；或者使用 vector）存储计算结果——从数组中取到 0（C 数组）或者下标不存在（vector）就说明没有缓存，有非零数字就是有缓存可以直接使用。

~~想不到吧这上面的全是作业（邪恶の笑）~~

8.7 De la lambda, je tombe le masque: Lambda 表达式（可选）
#

Lambda 表达式是 C++11 引入的一种创建匿名函数对象的方式。所谓 “匿名”，就是没有名字的函数。这允许我们在需要函数的地方就地定义函数，而不必先声明再定义。

Lambda 的内部其实是类，重载了 () 运算符使得看起来可以被调用（还有一个类似的 std::function，但是我们暂不深入）。不过我们可以不关心内部实现。毕竟如果一个东西声明像函数，调用像函数，返回像函数，那它就是函数（花火音）。或者严谨一点，叫做 函子（functor）。

不过我更习惯另一个翻译：函数对象，以区别于 Haskell 的函子（也是 Functor），两者数学起源相同但差别很大。

8.7.1 语法
#

Lambda 表达式的基本格式如下：

[捕获列表](参数列表) -> 返回类型 {
    函数体
}

简要解释：

捕获列表 指定了 Lambda 表达式可以访问哪些 外部变量（也有拷贝和引用两种方式）
参数列表 和普通函数的参数列表类似
返回类型 也和普通函数差不多，不过可以省略，编译器会自动推导
- 但建议明确写出来，特别是一眼看不出来的时候
举一些栗子，我们先不涉及捕获列表：

#include <iostream>
using namespace std;

int main() {
    // 最简单的lambda：无参，无返回
    []() {
        cout << "Hello, Lambda!" << endl;
    }(); // 尾部括号()表示（就在这里）调用，这和普通函数一样
    
    // 带参数的lambda，函数（地址）被赋予给add的变量
    auto add = [](int a, int b) -> int {
        return a + b;
    };
    
    cout << "3 + 5 = " << add(3, 5) << endl;
    
    // 省略箭头，自动推导返回类型
    auto multiply = [](double x, double y) {
        return x * y;
    };
    
    cout << "2.5 * 4 = " << multiply(2.5, 4) << endl;
    
    return 0;
}

8.7.2 捕获列表的妙用
#

捕获列表让 lambda 能够访问外部变量，如前所述，捕获和参数一样，有按值捕获和引用捕获两种，也可以理解为自动生成的“参数”。不过，“按值捕获”得到的是 只读的，不能修改。

我们直接一图码流：

#include <iostream>
using namespace std;

int main() {
    int x = 10;
    int y = 20;
    
    // 下面俩都称为“显式捕获”
    // 因为明确了到底捕获了哪些
    
    // 按值捕获：捕获外部变量的副本
    // 直接填写就是按值捕获
    auto capture_by_value = [x]() {
        cout << "Captured by value: " << x << endl;
        // x = 100; // 错误：不能修改值捕获的变量
    };
    capture_by_value();
    
    // 引用捕获：捕获外部变量的引用
    // 使用&表示引用，和普通参数一样
    auto capture_by_reference = [&y]() {
        cout << "Captured by reference: " << y << endl;
        y = 200; // 可以修改原变量
    };
    capture_by_reference();
    cout << "y after lambda: " << y << endl;
    
    // 下面俩都称为“隐式捕获”
    // 因为没有明确到底捕获了哪些
    // 是下大包围
    
    // 捕获所有外部变量（值方式）
    // 使用一个“=”
    auto capture_all_by_value = [=]() {
        cout << "All by value: x=" << x << ", y=" << y << endl;
    };
    capture_all_by_value();
    
    // 捕获所有外部变量（引用方式）
    // 使用一个“&”
    // 不建议这样！因为如果你不小心写了一个和外部相同的变量名
    // 就会修改到外部变量，给自己一个SURPRISE
    auto capture_all_by_reference = [&]() {
        x = 1000;
        y = 2000;
    };
    capture_all_by_reference();
    cout << "After all reference: x=" << x << ", y=" << y << endl;
    
    return 0;
}

输出：

Captured by value: 10
Captured by reference: 20
y after lambda: 200
All by value: x=10, y=200
After all reference: x=1000, y=2000

读者可以自行推导其中的过程。

显式捕获和隐式捕获可以混用，但不能和同类型的显式捕获一起使用，比如 [a, &b] 就是按值捕获 a，引用捕获 b；也有排除法：[=, &a] 就是全部按值捕获，除了 a 是按引用捕获。诸如 [=, &]（《朝令夕改》），[&, &a]（《多此一举》）都是不合理的。

“按值捕获”得到的是只读的，如果想要修改按值捕获的变量，可以使用 mutable 关键字，不过其效果与你预想的可能不太一样，mutable 以后得到的值在 lambda 结束后还可以一直存在，直到调用者（这里是 main）结束才会被销毁，比如下面的例子就展示了这个坑：

#include <iostream>
using namespace std;

int main() {
    int count = 0;
    
    // 使用mutable允许修改值捕获的变量
    auto counter = [count]() mutable {
        count++;
        cout << "Count inside lambda: " << count << endl;
        return count;
    };
    
    counter();
    counter();
    counter();
    
    cout << "Original count: " << count << endl;
    
    return 0;
}

输出：

Count inside lambda: 1
Count inside lambda: 2
Count inside lambda: 3
Original count: 0

这种现象的原因是 lambda 函数内部实现是一个类，这个类的生命周期和调用者一样长，所以counter 内部的 count 的拷贝暂时不会被销毁，从而没有出现三次都是“Count inside lambda: 1”的现象。

8.7.3 Lambda 跳出多重循环的例子
#

还记得我们在循环章节提到的跳出多重循环的问题吗？Lambda 提供了一种优雅的解决方案：

#include <iostream>
#include <vector>
using namespace std;

int main() {
    // 一个3*3的二维数组
    // 我们尝试遍历并找到目标5
    vector<vector<int>> matrix = {
        {1, 2, 3},
        {4, 5, 6},
        {7, 8, 9}
    };
    
    int target = 5;
    bool found = false;
    
    // 使用lambda跳出多重循环
    [&matrix, target]() { 
        for (int i = 0; i < matrix.size(); i++) {
            for (int j = 0; j < matrix[i].size(); j++) {
                if (matrix[i][j] == target) {
                    cout << "找到目标值 " << target 
                         << " 在位置 (" << i << ", " << j << ")" << endl;
                    found = true;
                    return; // 直接从lambda返回，跳出所有循环
                }
            }
        }
    }(); // 立即调用
    
    if (!found) {
        cout << "未找到目标值 " << target << endl;
    }
    
    return 0;
}

这样就可以避免 goto。当然，你也可以使用标志变量，一旦找到，就设置这个变量的值为假（或者真，无所谓），一旦这个变量的值为假（或者真），所有循环都结束。这个具体代码留到课后习题。

另外，函数还有内联修饰符 inline，参阅 12.3 结尾。

8.8 小结
#

这个章节实在很长，我们特地总结一下。其实后面会越来越长。——作者CommandPrompt于第二次修订

函数的舞台丰富多彩，函数可以独自登台，也可以一人千役；函数的剧本（参数）多种多样……还有递归、lambda 表达式等较为复杂精彩的戏码等待我们进一步发掘。而每一种技法都是我们手中不可或缺的利器，等待着我们在更多场景中发挥其精妙之处。

课后作业：

模仿 8.3 结尾的模板，定义一个泛型交换函数 mySwap()。
首先尝试使用引用传递，然后考虑使用指针传递再实现一次。
比较两者函数定义和调用的共性和差异。
使用递归编写一个阶乘函数，并分别计算 1~10 的阶乘值。
尝试写一个使用循环的版本。
使用递归编写一个斐波那契函数，并计算第 40 项。尝试使用尾递归和记忆化
尝试写一个使用循环的版本，并比较4个版本的运行速率。（尾递归想不到可以参考答案的思路，涉及用参数向下传递信息）
使用递归编写一个倒序字符串（使用 std::string，用法和普通 char 差不多）的函数。尝试使用尾递归。
提示，假设你的声明是 std::string str;，试试在 str 后面打一个 .（英文点），看看代码补全会弹出什么。

可能用到的方法（就是 str.xxx() 的 xxx）：
- pop_front()：弹出第一个字符并返回这个字符（std::string str = "123456"; char c = str.pop_front(); 这样 str 是 23456，而 c 是 1）
- pop_back()：弹出最后一个字符并返回这个字符
使用递归完成汉诺塔问题
有三个班级（1,2,3），每个班有若干个学生。数据结构如下（可以直接拿来用）：
```
vector<vector<string>> matrix = {
    {"张三", "李四", "王五"},
    {"赵六", "孙七", "周八"},
    {"吴九", "郑十", "刘一"},
    {"陈二", "黄三", "林四"}
};
```
尝试模仿着遍历这个数组，使用 lambda 退出二重循环。并尝试实现 8.7.3 提到的使用标志变量的方法。

作者

命令提示符@CommandPrompt-Wang

8.1 函数千面，奔走人间 #

8.2 Le clou du spectacle: 函数的声明与定义 #

8.3 La déesse aux cent miracles: 函数的重载（C++） #

8.4 La marée s‘invite à la fête: 函数的参数 #

8.4.1 按值传递 #

8.4.2 指针传递 #

8.4.3 引用传递 #

8.4.4 形参和实参 #

8.5 Acta est fabula, plaudite: 函数的返回 #

8.6 Dans l’eau, doublement je me reflète: 递归 #

8.7 De la lambda, je tombe le masque: Lambda 表达式（可选） #

8.7.1 语法 #

8.7.2 捕获列表的妙用 #

8.7.3 Lambda 跳出多重循环的例子 #

8.8 小结 #